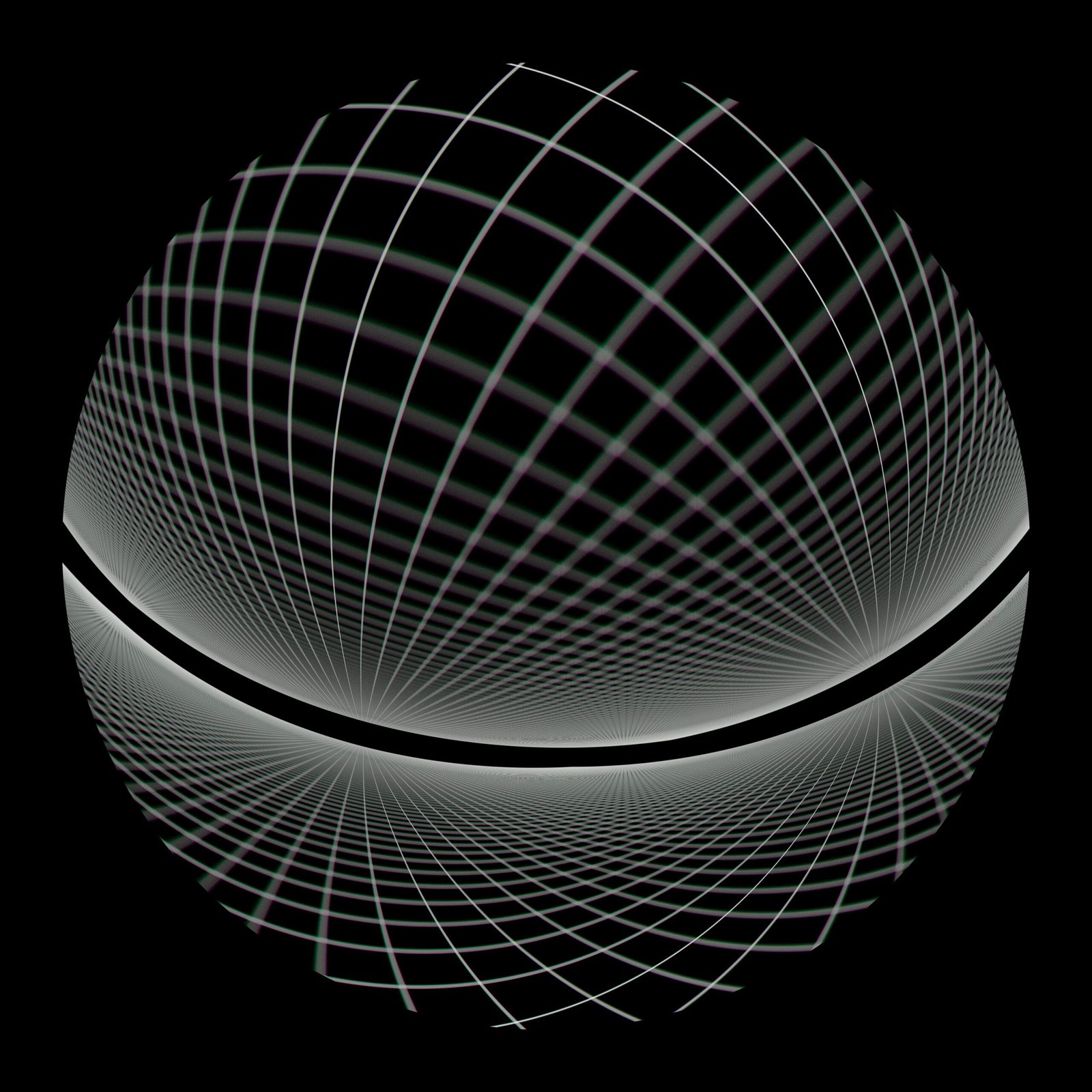
Have you ever marveled at a structure that seems to defy gravity or challenged your understanding of curves? Enter the world of the hyperbolic paraboloid, a fascinating shape that combines beauty with complexity. This unique geometric form is often described as a “saddle,” but its allure goes far beyond mere functionality. From architecture to art, it captures our imagination and challenges conventional design norms. Whether you’re an aspiring architect, a mathematics enthusiast, or simply curious about shapes in nature, joining us on this exploration will open your eyes to the elegance and versatility of the hyperbolic paraboloid. Let’s dive into its history, applications, and much more!
Understanding the Hyperbolic Paraboloid
The hyperbolic paraboloid is a fascinating geometric surface. It can be defined mathematically by the equation \( z = \frac{x^2}{a^2} – \frac{y^2}{b^2} \). This formula reveals its unique saddle shape, characterized by one curvature facing upwards and another downwards.
Visually, it appears as if the surface dips in one direction while rising in another. This duality makes it distinct from other quadric surfaces like ellipsoids or parabolas.
You’ll often find this form in various fields of study, from mathematics to architecture. Its structural properties allow for efficient load distribution, making it ideal for modern buildings and roofs.
Moreover, this intriguing geometry plays with perception; it challenges our understanding of what a curved surface can be. The hyperbolic paraboloid is more than just a shape—it’s an invitation to explore the crossroads of art and science.
History and Origin of Hyperbolic Paraboloids
The hyperbolic paraboloid, often described as a saddle-shaped surface, has roots that trace back to the 19th century. Mathematicians began exploring its unique properties during this period.
One of the earliest documented uses comes from German mathematician Karl Friedrich Gauss. His work laid foundational principles in differential geometry, paving the way for further studies on curved surfaces.
As architectural innovation surged in the mid-20th century, designers embraced hyperbolic paraboloids for their structural efficiency and aesthetic appeal. The shape became synonymous with modernist architecture.
Notably, buildings like the TWA Flight Center at JFK Airport showcased this form’s elegance while also addressing practical engineering challenges. The interplay between mathematics and art continued to unfold as artists and architects explored these captivating structures throughout history.
Real-life Applications of Hyperbolic Paraboloids
Hyperbolic paraboloids are not just mathematical constructs; they have fascinating real-world applications. Their unique shape, resembling a saddle, allows for structural efficiency and aesthetics in various fields.
In architecture, buildings like the renowned TWA Flight Center at JFK Airport showcase sweeping roofs that utilize this geometry. The design minimizes material while maximizing strength—a win-win in construction.
These shapes also find their way into engineering projects. Bridges and canopies often incorporate hyperbolic paraboloid designs to provide both shelter and visual appeal.
Even in product design, furniture pieces such as tables exhibit these curves for ergonomic comfort combined with striking looks.
Art installations sometimes employ hyperbolic forms to create dynamic sculptures that engage viewers from different angles. This versatility makes the hyperbolic paraboloid an exciting subject matter across disciplines.
How to Construct a Hyperbolic Paraboloid
Constructing a hyperbolic paraboloid can be an exciting challenge. It starts with selecting two sets of parallel lines that will define the surface’s shape.
Begin by drawing two intersecting grids, one representing the x-axis and another for the y-axis. The intersection points create a network of coordinates to work from.
Next, use flexible materials like wire or thin sheets to outline curves between these points. This flexibility allows you to achieve that signature saddle shape characteristic of hyperbolic paraboloids.
Once your framework is ready, skin it with lightweight materials such as fabric or plywood. These surfaces should follow the curvature defined by your initial grid layout.
Ensure stability by reinforcing joints where necessary. A well-constructed model showcases not only geometric beauty but also structural integrity in its design.
The Beauty of the Hyperbolic Paraboloid in Architecture and Art
The hyperbolic paraboloid captivates architects and artists alike with its distinctive shape. Its saddle-like geometry creates a striking visual impact, making it a favorite in contemporary design.
Structures like the iconic Sydney Opera House showcase this form’s elegance. The sweeping curves draw the eye upward, embodying both grace and strength.
In art, this shape inspires sculptures that play with light and shadow. Artists use the hyperbolic paraboloid to evoke movement and dynamism, inviting viewers to engage from different angles.
Public spaces benefit too; parks and pavilions often incorporate this form for aesthetic appeal while providing functional benefits such as natural lighting or acoustic advantages.
The blend of mathematical precision with organic beauty makes the hyperbolic paraboloid a true marvel in creative spheres. It encourages innovation by pushing boundaries in both architecture and artistic expression.
Limitations and Challenges in Working with Hyperbolic Paraboloids
Working with hyperbolic paraboloids presents unique challenges. Their distinctive saddle shape can complicate various engineering and architectural processes.
Material selection becomes critical, as not all materials can effectively support the curved surfaces. Finding the right balance between strength and flexibility often requires extensive testing.
Construction techniques must also adapt to these complex geometries. Skilled labor is essential for accurate execution, which may lead to higher costs and project timelines.
Moreover, achieving precise mathematical calculations is vital but challenging. Any miscalculation in dimensions could result in structural weaknesses or aesthetic discrepancies.
Understanding how light interacts with these surfaces adds another layer of complexity. The play of shadows and reflections needs careful consideration to achieve desired visual effects in design projects.
Conclusion: Appreciating the Complexity and Creativity of the Hyperbolic Paraboloid
The hyperbolic paraboloid stands out as a remarkable shape that transcends simple geometry. Its unique structure, characterized by its saddle-like form, invites both mathematicians and artists to explore its depths. The interplay of curves and surfaces offers endless possibilities for innovation.
This fascinating geometric figure is not only intriguing mathematically but also holds significant aesthetic value. From modern architecture to intricate sculptures, the hyperbolic paraboloid inspires creativity in various fields. It captures the imagination through its elegant lines and dynamic forms.
Engaging with this shape encourages a deeper appreciation for the complexities present in mathematics and design. Whether you encounter it in structural engineering or artistic expression, the hyperbolic paraboloid serves as a reminder of how beauty can stem from mathematical principles. Embracing such geometries enriches our understanding of both art and science, showcasing an extraordinary blend of creativity and precision that continues to inspire future generations.